Q-value functions

×

Q tabulaire

Structure

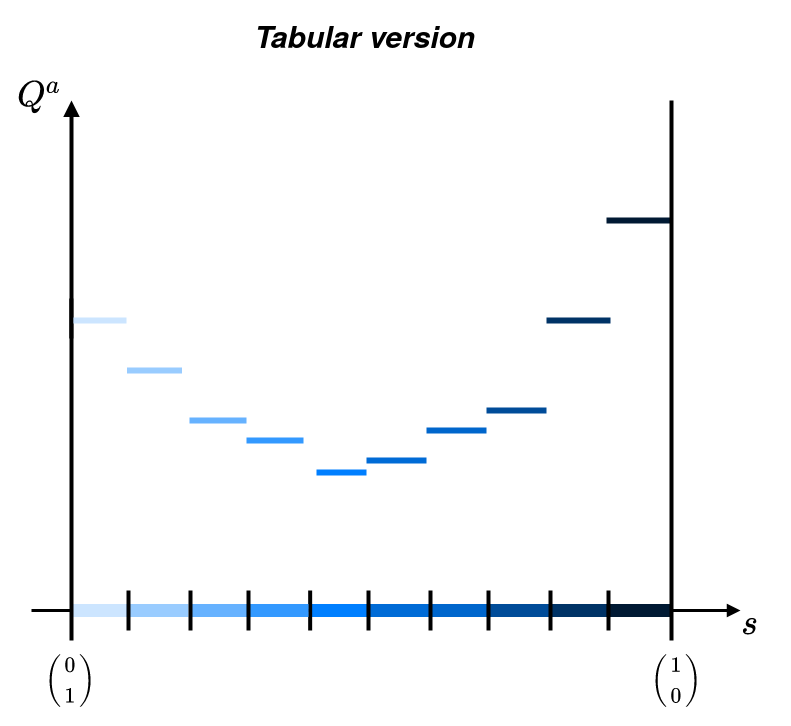
La fonction de $Q$ la plus simple est la fonction tabulaire. On la représente par une simple matrice dont les lignes représentent les états et les colonnes les actions. Cette fonction est parfaitement appropriée pour les cas où les espace d'état et d'action sont discrets et relativement petits. En effet, dans le cas d'un espace d'état (resp. espace d'action) continu, le nombre de valeurs à stoker tendra vers l'infinie. Pour faire face à ce problème, nous devons définir une distance entre les états (resp. les actions) qui garantisse l'obtention d'une matrice de dimension finie.

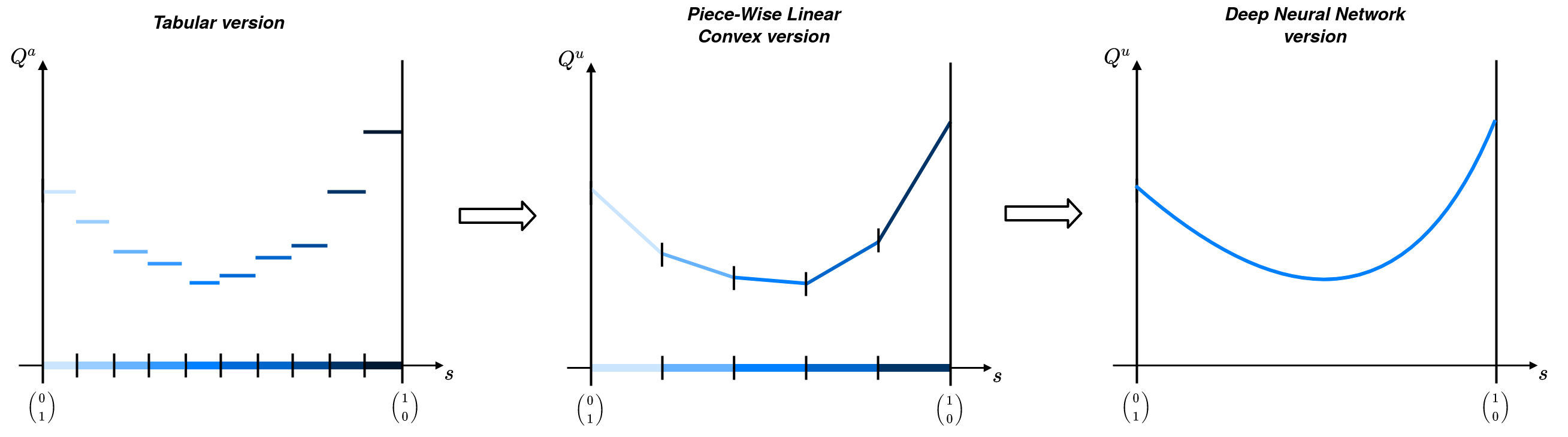
En prenant le cas d'une statistique suffisante $s$ définit sur le $(n+1)$-simplexe (i.e $s \in [0,1]^n$ et $\sum_{x=1}^n s(x) = 1$), la fonction de valeur tabulaire pourrait être représentée comme ci-dessous.

Evaluation

L'évaluation d'un nouveau point $s$ est dépendant de la boule d'appartenance de ce dernier.

Update operator

Dans ce cas, la mise à jour de la fonction de valeur relative à l'algorithme du Q-learning s'écrit comme ci-dessous.

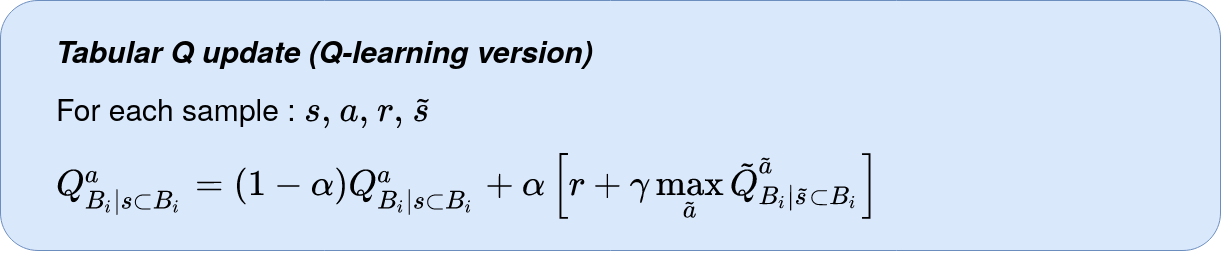
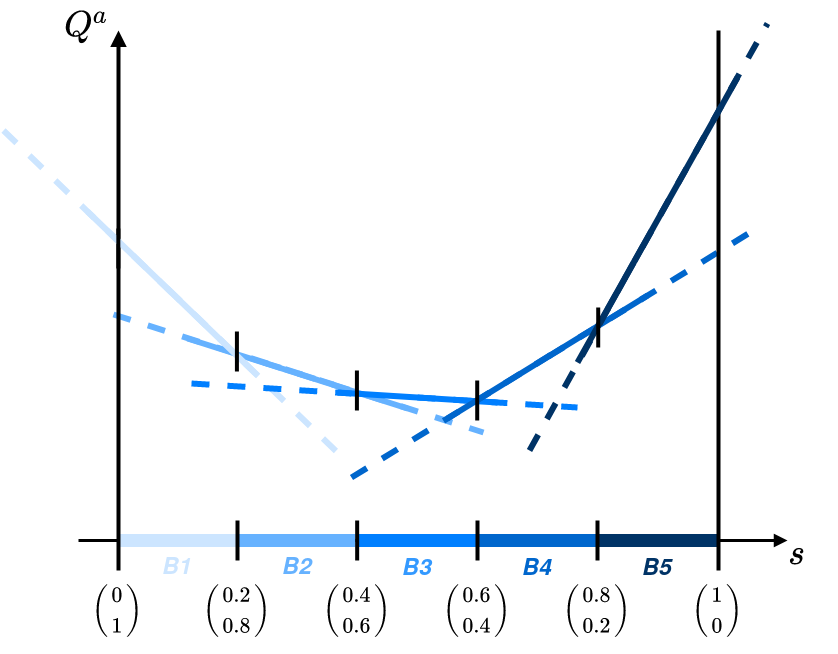
PWLC Q

Structure

Prenons le cas général d'une statistique suffisante $s$ définit sur le $(n+1)$-simplexe (i.e $s \in [0,1]^n$ et $\sum_{x=1}^n s(x) = 1$).

Pour toute action, notée $a$, la fonction de valeur $Q^a : [0,1]^n \rightarrow \mathbb{R}$ est convexe et linéaire par morceaux. On peut donc l'approximer grâce à un ensemble d'hyperplans définis sur le simplexe. Une des représentation utilisée dans SDMS consiste à réaliser un mapping entre des boules $B_i$ sur le simplexe et un hyperplan qui leur est associé.

Evaluation

L'évaluation d'un nouveau point $s$ est dépendant de la boule d'appartenance de ce dernier.

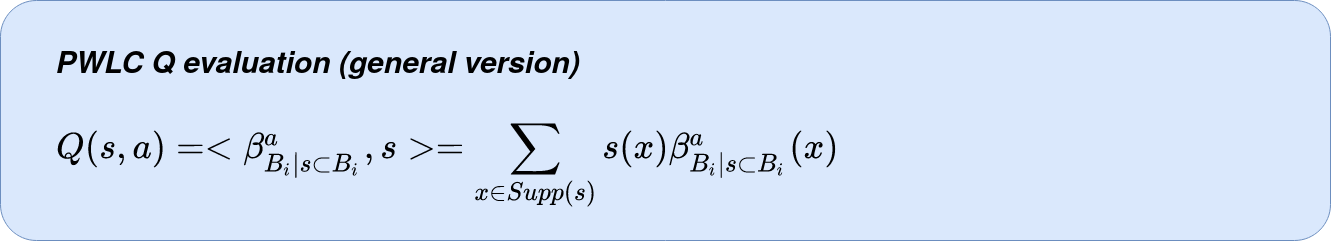
Update operator

La mise à jour de la fonction de valeur dans ce cas s'écrit comme ci-dessous.

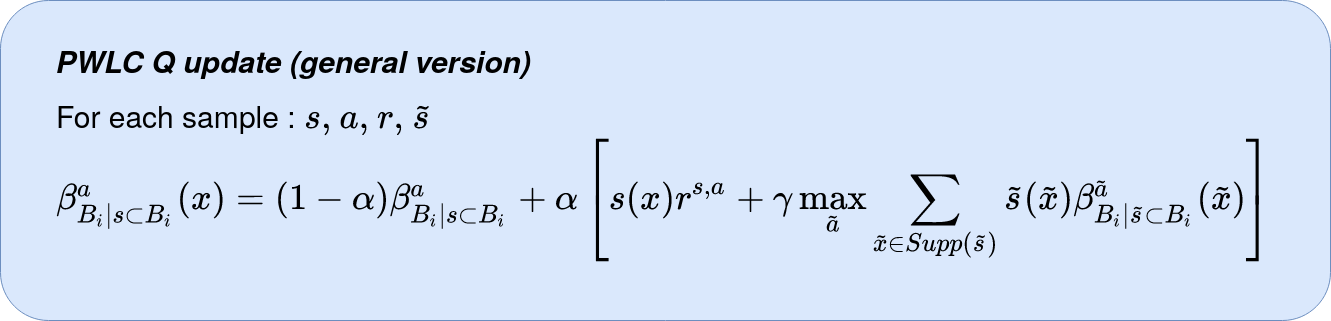
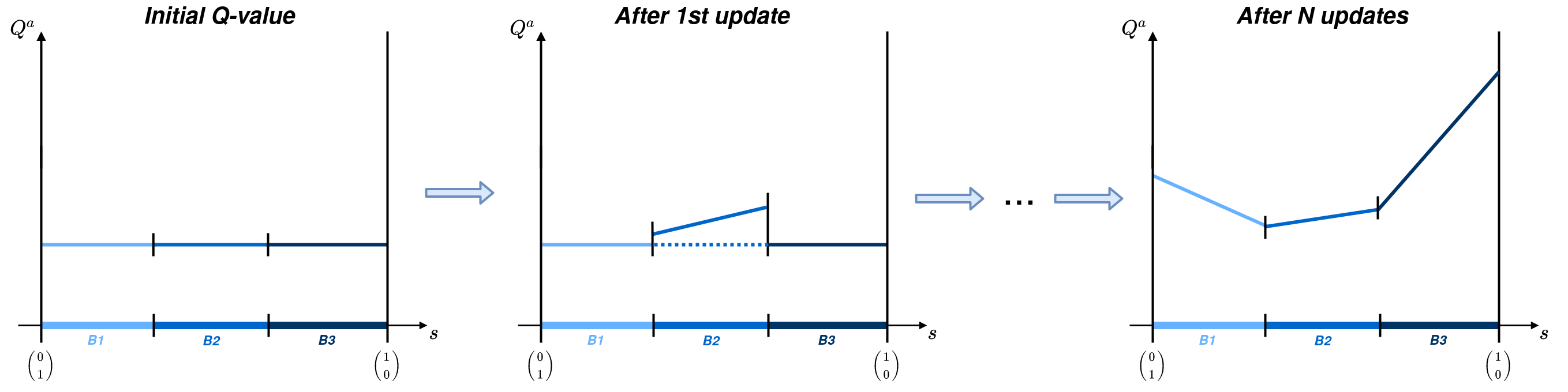
Lors de l'apprentissage, la fonction de valeur sera mise à jour successivement et selon les échantillons générés. Un exemple d'exécution pourrait ressembler à la figure suivante:

×

Deep Q