Value functions

Tabular Value

Structure

×

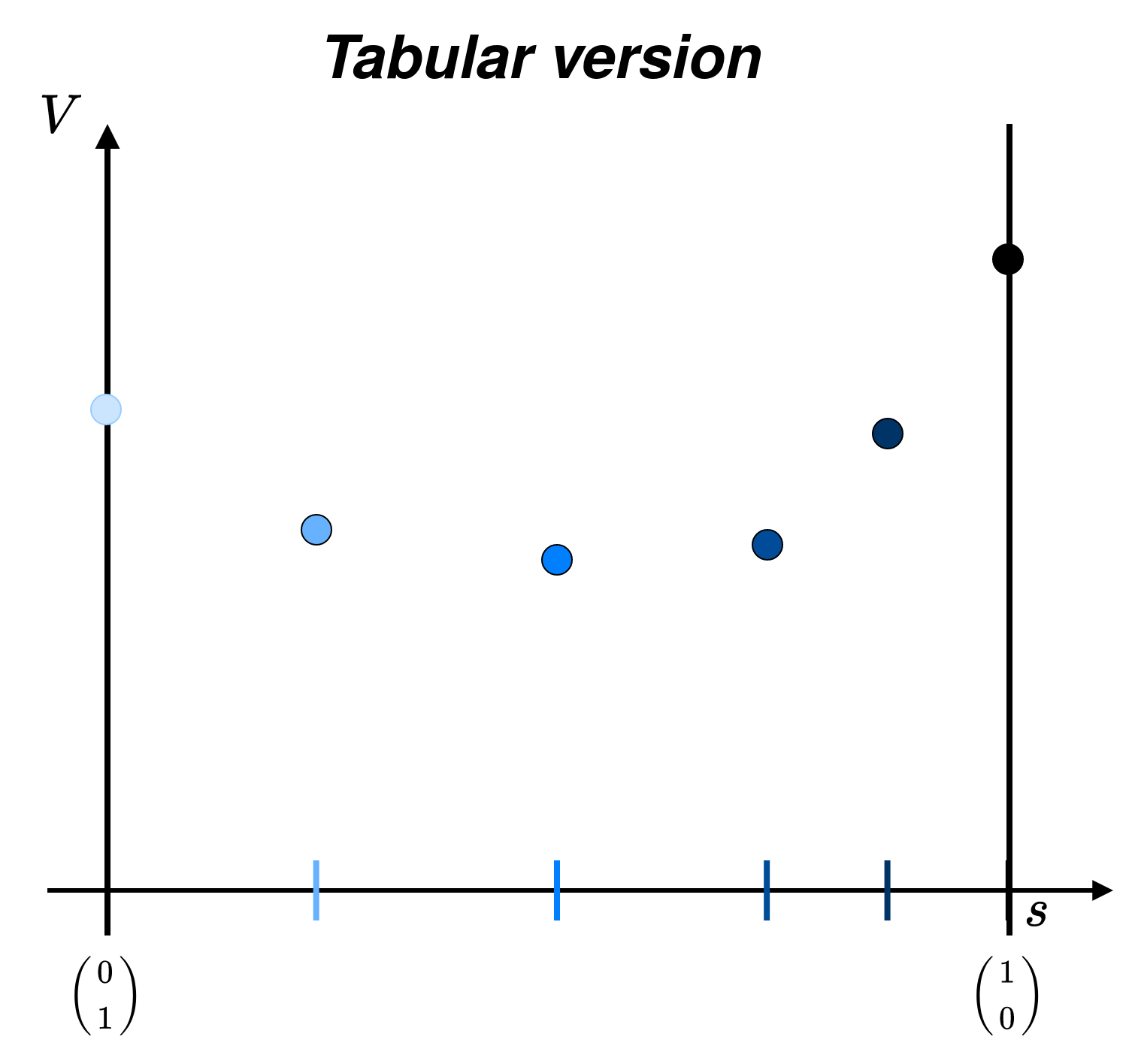
Evaluation

L'évaluation d'un nouveau point $s$ est la valeur du tableau correspondant à ce point.

$V(s)=V_{i_s}$ where $i_s$ is the index of the state in the table

Update operator

PWLC Value

Structure

Prenons le cas général d'une statistique suffisante $s$ définit sur le $(n+1)$-simplexe (i.e $s \in [0,1]^n$ et $\sum_{x=1}^n s(x) = 1$).

La fonction de valeur $V : [0,1]^n \rightarrow \mathbb{R}$ est convexe et linéaire par morceaux. On peut donc l'approximer grâce à un ensemble d'hyperplans définis sur le simplexe. Une des représentation utilisée dans SDMS consiste à garder un ensemble d'hyperplans, noté $\Gamma_{\alpha}$, sur le simplexe.

×

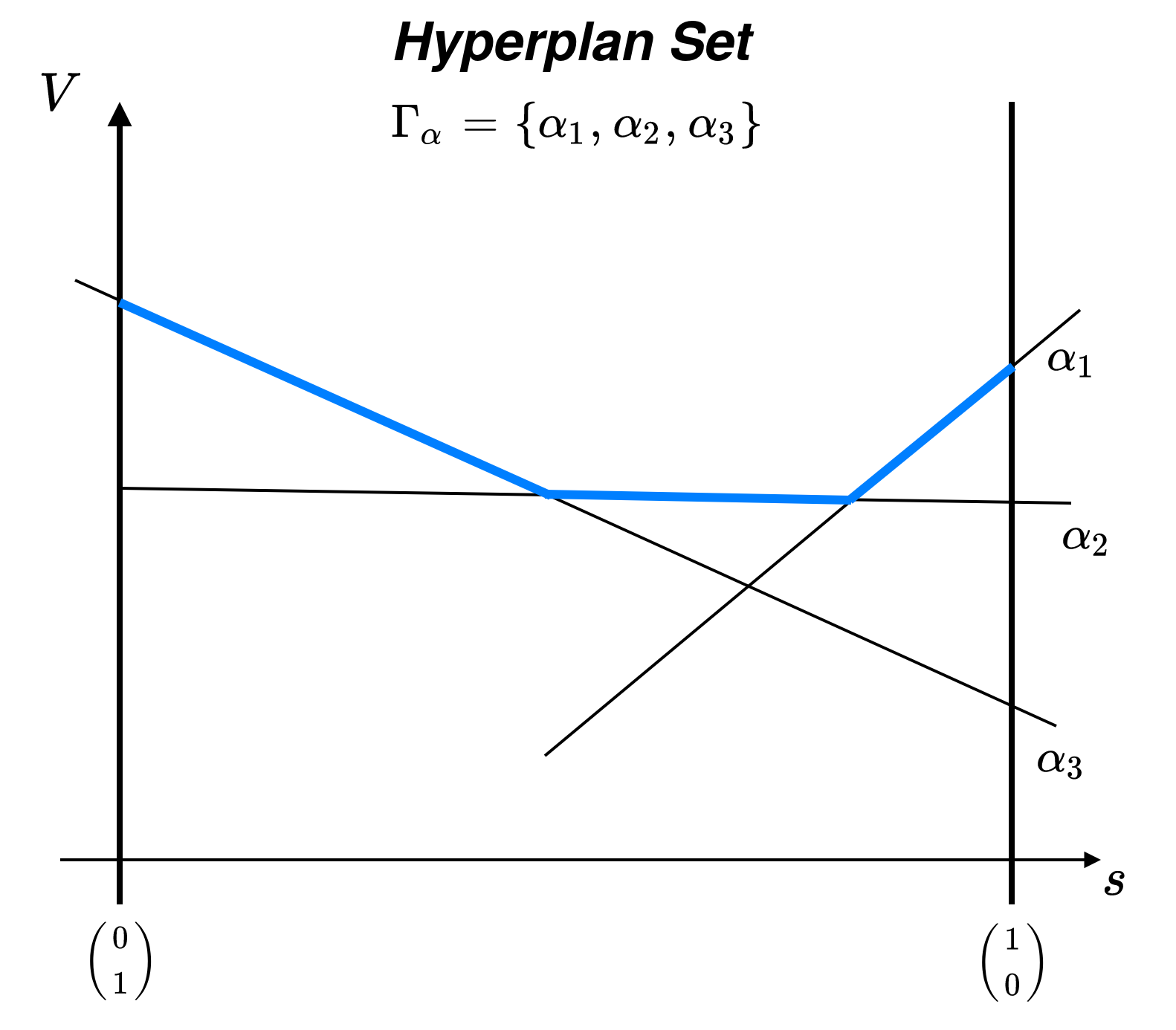
Evaluation

L'évaluation d'un nouveau point $s$ est dépendant de la boule d'appartenance de ce dernier.

$V(s)=\max_{\alpha \in \Gamma_{\alpha}} \alpha \bullet s = max_{\alpha \in \Gamma_{\alpha}} \sum_{x \in Supp(s)} \alpha (x) s(x)$

Update operator

×

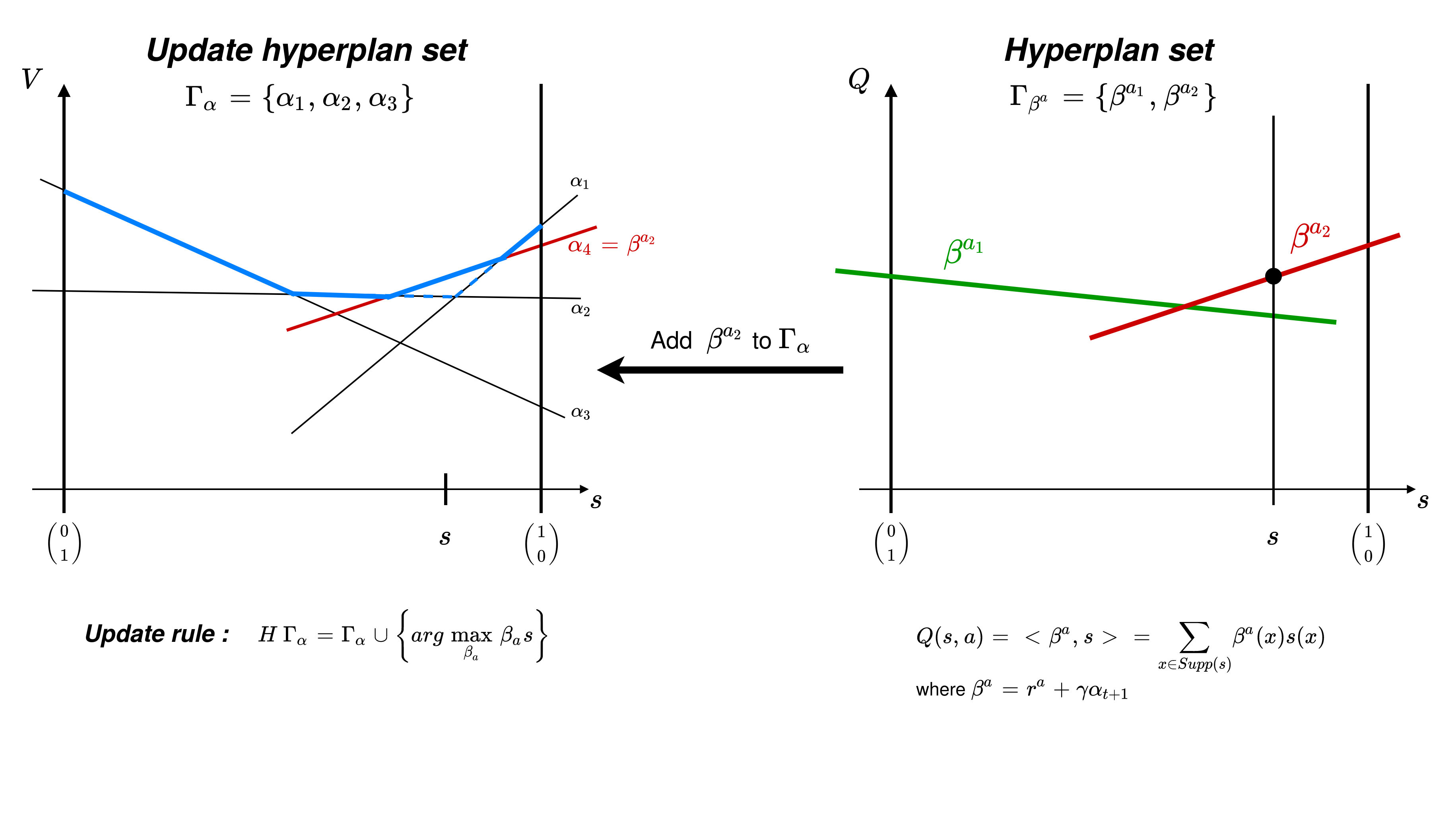
Sawtooth Value

Evaluation

L'évaluation d'un nouveau point $s$ est une interpolation entre les points existants.

$V(s) = V^{relax}(s) + \min_{\kappa} \left[ \min_{x\in Supp(s^{\kappa})} \left[ \frac{s(x)}{s^{\kappa}(x)} \left( V^{relax}(s^{\kappa}) - V^{\kappa} \right)\right] \right]$