Q-value functions

×

Tabular Q

Structure

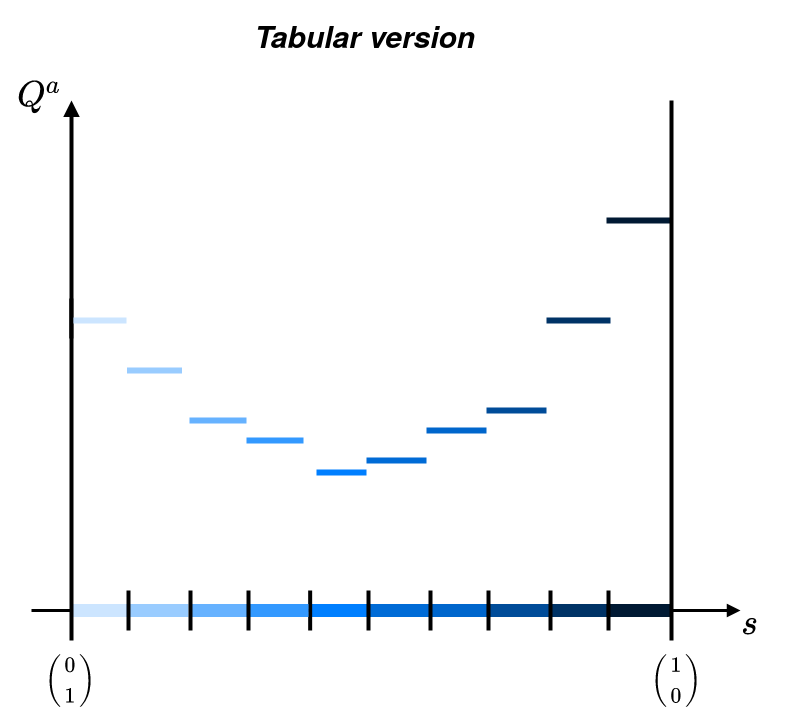
The simplest function of $Q$ is the tabular function. It is represented by a simple matrix whose rows represent the states and columns the actions. This function is perfectly appropriate for cases where the state and action spaces are discrete and relatively small. Indeed, in the case of a continuous state (resp. action) space, the number of values to be stoked will tend to infinity. To face this problem, we have to define a distance between states (resp. actions) that guarantees the obtaining of a finite dimensional matrix.

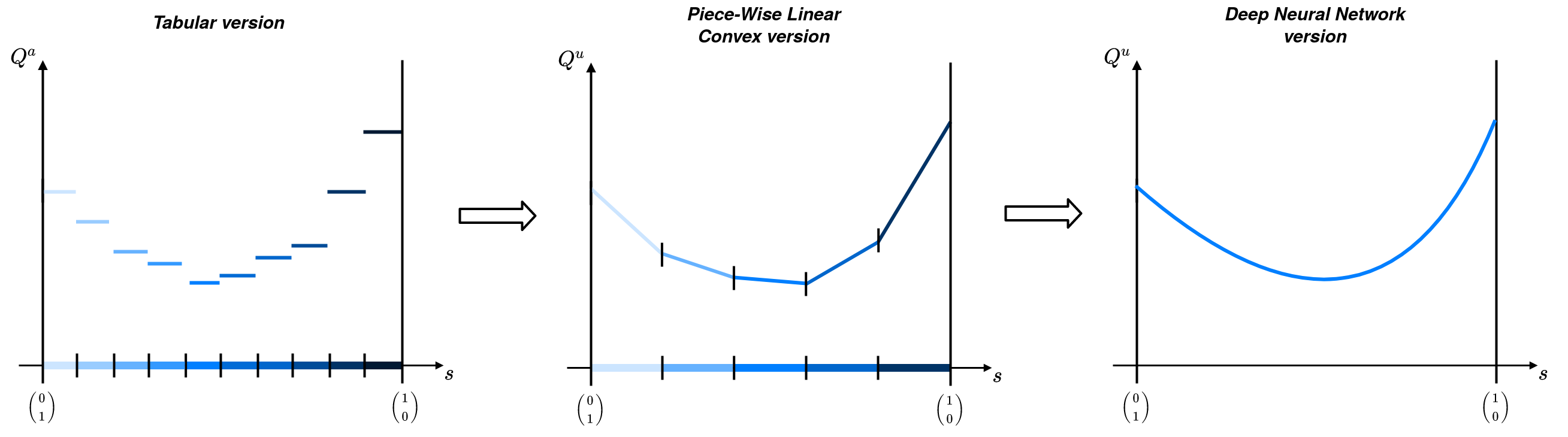
Considering the case of a sufficient statistic $s$ defined on the $(n+1)$-simplex (i.e. $s \in [0,1]^n$ and $sum_{x=1}^n s(x) = 1$), the tabular value function could be represented as below.

Evaluation

The evaluation of a new point $s$ depends on the ball it belongs to.

Update operator

In this case, the update of the value function for the Q-learning algorithm is written as follows.

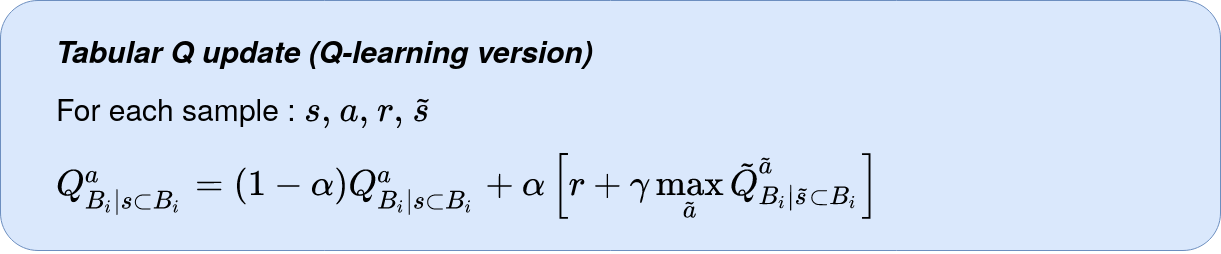
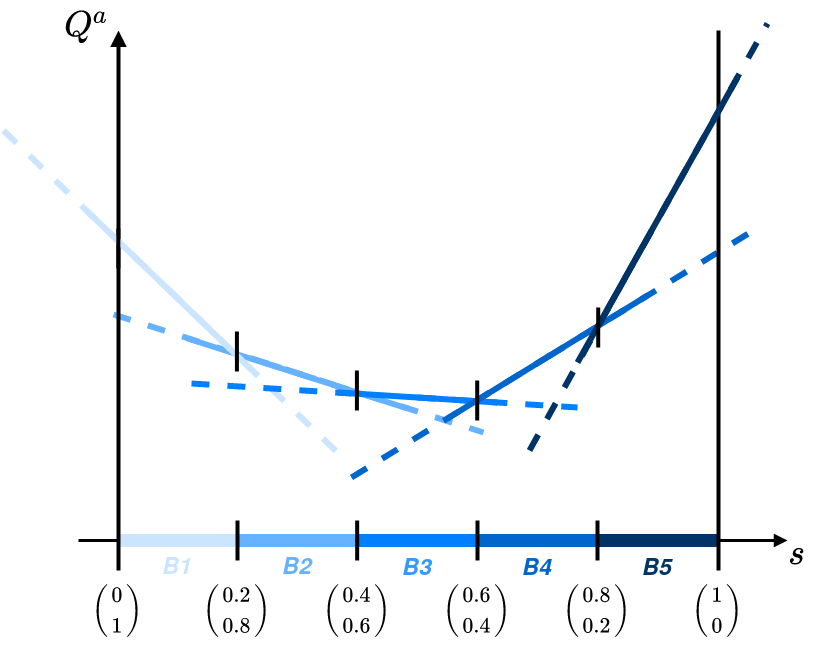
PWLC Q

Structure

Consider the general case of a sufficient statistic $s$ defined on the $(n+1)$-simplex (i.e. $s \in [0,1]^n$ and $sum_{x=1}^n s(x) = 1$).

For any action, denoted $a$, the value function $Q^a : [0,1]^n \rightarrow \mathbb{R}$ is convex and piecewise linear. It can therefore be approximated by a set of hyperplanes defined on the simplex. One of the representations used in SDMS consists in mapping $B_i$ balls on the simplex to an associated hyperplane.

Evaluation

The evaluation of a new point $s$ depends on the ball it belongs to.

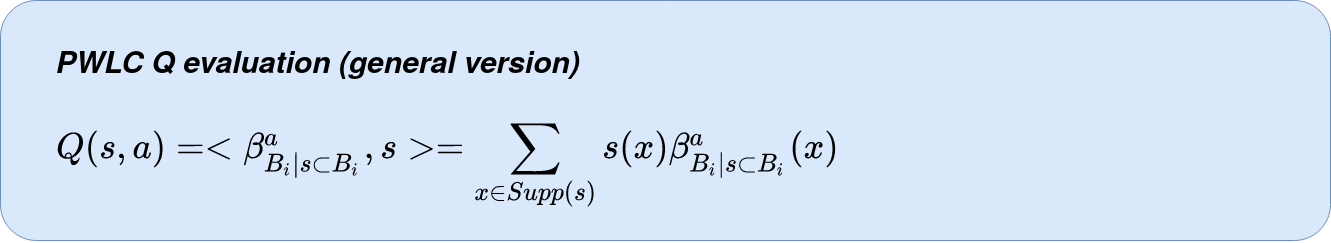
Update operator

The update of the value function in this case is written as follows.

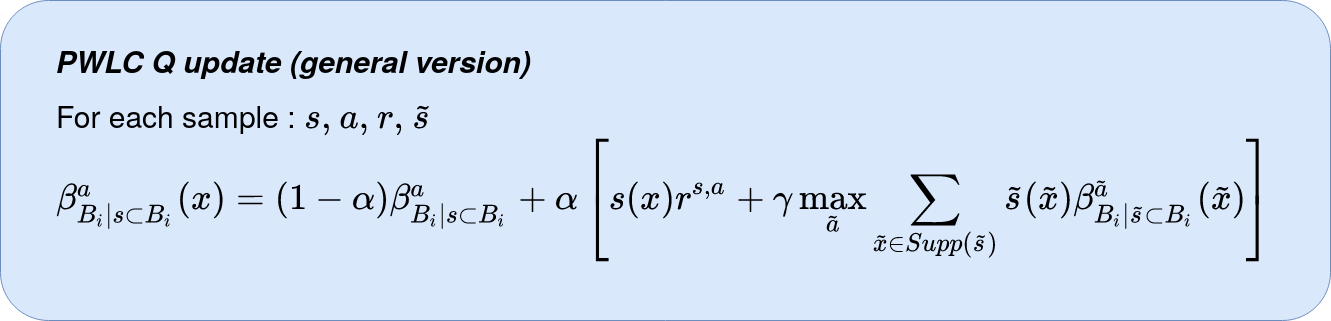
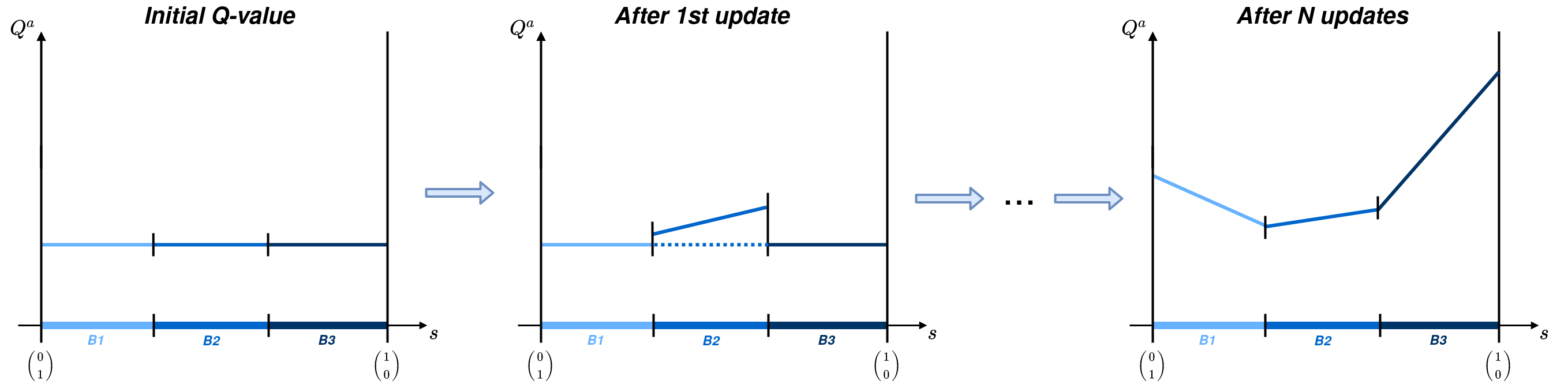
During training, the value function will be updated successively and according to the generated samples. An example of execution could look like the following figure:

×

Deep Q