Algorithmic foundations

The SDM'Studio platform is built around the genericity of algorithmic schemes for planning and reinforcement learning. The platform's native algorithmic schemes are HSVI and Q-learning. However, the list is extended to other state-of-the-art algorithms.

	A*	Backward Induction	HSVI	MCTS	PBVI	Perseus	Q-Learning	REINFORCE	SARSA	Value Iteration
MDP	🚫	✅	✅	❌	🚫	🚫	✅	❌	✅	✅
serial MMDP	🚫	✅	✅	❌	🚫	🚫	✅	❌	✅	✅
belief MDP	❌	✅	✅	❌	✅	✅	✅	❌	✅	🚫
serial belief MDP	❌	✅	✅	❌	✅	✅	✅	❌	✅	🚫
hierarchical belief MDP	❌	✅	✅	❌	✅	✅	✅	❌	✅	🚫
occupancy MDP	✅	✅	✅	❌	✅	✅	✅	❌	✅	🚫
serial occupancy MDP	❌	✅	✅	❌	✅	✅	✅	❌	✅	🚫
hierarchical occupancy MDP	❌	✅	✅	❌	✅	✅	✅	❌	✅	🚫
OccupancyMG	❌	❌	❌	❌	❌	❌	❌	❌	❌	🚫

Legend : ❌ not implemented 🚫 not allowed ✅ implemented

Algorithmic patterns can be seen as generic templates. Each instance of one of these schemes is an algorithm in its own right. The changes may occur in the problem definition or in the way the value functions are represented.

HSVI algorithmic scheme

The general algorithmic scheme of HSVI is represented by the diagram below. To define an instance, this one requires to define the notions of state $s_t$, action $a_t$, lower bound $underline{V}$ and upper bound $bar{V}$.

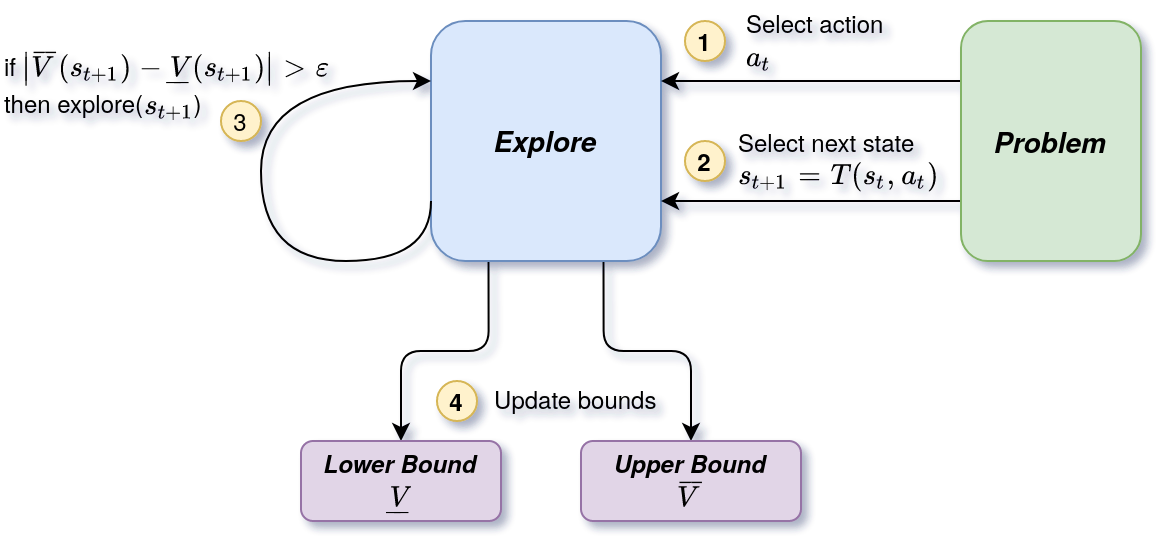
Example : An instance of HSVI is the oHSVI algorithm. This instance allows to solve a Dec-POMDP formulated as an occupancy-state MDP. The state type in this case is an occupancy state, noted $xi_t = p\left( x_t, o_t \mid \iota_t \right)$. The action type is a set of individual decision rules, denoted $\mathbf{d}_t = (d_t^1, ..., d_t^n) = \left(p(u^1 \mid o_t^1), p(u^2 \mid o_t^2),..., p(u^n \mid o_t^n)\right)$. The lower bound is represented by a set of hyperplanes and the upper bound by a set of points.

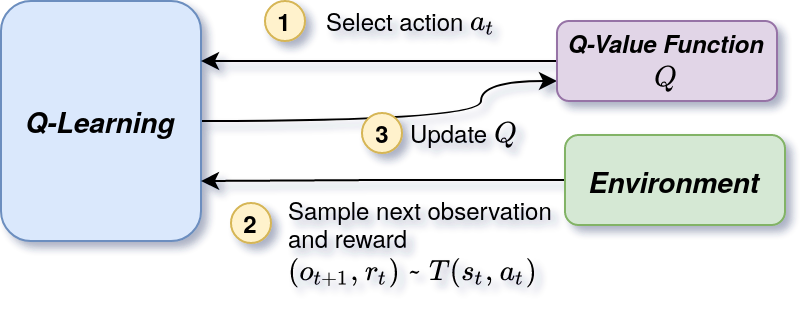
Q-learning algorithmic scheme

The general algorithmic scheme of Q-learning requires the definition of the notions of state, action and action value function (Q-value).